前缀和与差分的应用

前缀和：P10904 [蓝桥杯 2024 省 C] 挖矿

题目描述

小蓝正在数轴上挖矿，数轴上一共有 $n$ 个矿洞，第 $i$ 个矿洞的坐标为 $a_i$。小蓝从 $0$ 出发，每次可以向左或向右移动 $1$ 的距离，当路过一个矿洞时，就会进行挖矿作业，获得 $1$ 单位矿石，但一个矿洞不能被多次挖掘。小蓝想知道在移动距离不超过 $m$ 的前提下，最多能获得多少单位矿石？

输入格式

输入的第一行包含两个正整数 $n,m$，用一个空格分隔。

第二行包含 $n$ 个整数 $a_1, a_2,\cdots, a_n$，相邻整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示答案。

输入输出样例 #1

输入 #1

5 4
0 -3 -1 1 2

输出 #1

4

说明/提示

【样例说明】

路径：$0\to -1\to 0\to 1\to 2$，可以对 $\{0,-1,1,2\}$ 四个矿洞挖掘并获得最多 $4$ 块矿石。

【评测用例规模与约定】

对于 $20\%$ 的评测用例，$1 \le n \le 10^3$；
对于所有评测用例，$1 \le n \le 10^5$，$-10^6 \le a_i \le 10^6$，$1 \le m \le 2 \times 10^6$。

解决方案

在这道题的情景下，我们显然需要先判断哪个方向上的矿石数目多，哪个方向上的矿石数目多就往哪个方向上挖。同时再用一个变量或者数组来记录剩余的步数，每挖一个矿就检查剩余的步数，来确保能得到一个最优解。

而如果要判断哪个方向上剩余的矿石数目多，我们就可以使用前缀和的方法。

def main():
  n, m = map(int, input().split())
  holes = list(map(int, input().split()))

  N = 2000005
  ls = [0] * N
  rs = [0] * N
  zeros = 0

  for hole in holes:
    if hole < 0:
      ls[-hole] += 1
    elif hole == 0:
      zeros += 1
    else:
      rs[hole] += 1

  # 计算前缀和
  # 这里i最大为m是朝一个方向最多只能走m步
  for i in range(1, m+1):
    ls[i] += ls[i-1]
    rs[i] += rs[i-1]

  # 有了前缀和之后开始枚举
  ans = 0
  for i in range(1, m+1):
      # 先枚举左边：
      count = ls[i]
      # 判断是否还能掉头挖矿：
      if m - 2 * i > 0:
        count += rs[m-2*i]
      
      ans = max(count, ans)

      # 再枚举右边
      count = rs[i]
      if m - 2 * i > 0:
        count += ls[m-2*i]
      
      ans = max(count, ans)

  ans += zeros

  print(ans)

if __name__ == "__main__":
  main()

Bingo!

差分：P10903 [蓝桥杯 2024 省 C] 商品库存管理

题目描述

在库存管理系统中，跟踪和调节商品库存量是关键任务之一。小蓝经营的仓库中存有多种商品，这些商品根据类别和规格被有序地分类并编号，编号范围从 $1$ 至 $n$。初始时，每种商品的库存量均为 $0$。

为了高效地监控和调整库存量，小蓝的管理团队设计了 $m$ 个操作，每个操作涉及到一个特定的商品区间，即一段连续的商品编号范围（例如区间 $[L, R]$）。执行这些操作时，区间内每种商品的库存量都将增加 $1$。然而，在某些情况下，管理团队可能会决定不执行某些操作，使得这些操作涉及的商品区间内的库存量不会发生改变，维持原有的状态。

现在，管理团队需要一个评估机制，来确定如果某个操作未被执行，那么最终会有多少种商品的库存量为 $0$。对此，请你为管理团队计算出，对于每个操作，如果不执行该操作而执行其它操作，库存量为 $0$ 的商品的种类数。

输入格式

输入的第一行包含两个整数 $n$ 和 $m$，分别表示商品的种类数和操作的个数。

接下来的 $m$ 行，每行包含两个整数 $L$ 和 $R$，表示一个操作涉及的商品区间。

输出格式

输出 $m$ 行，每行一个整数，第 $i$ 行的整数表示如果不执行第 $i$ 个操作，则最终库存量为 $0$ 的商品种类数。

输入输出样例 #1

输入 #1

5 3
1 2
2 4
3 5

输出 #1

1
0
1

说明/提示

【样例说明】

考虑不执行每个操作时，其余操作对商品库存的综合影响：

• 不执行操作 $1$：剩余的操作是操作 $2$（影响区间 $[2, 4]$）和操作 $3$（影响区间 $[3, 5]$）。执行这两个操作后，商品库存序列变为 $[0, 1, 2, 2, 1]$。在这种情况下，只有编号为 $1$ 的商品的库存量为 $0$。因此，库存量为 $0$ 的商品种类数为 $1$。

• 不执行操作 $2$：剩余的操作是操作 $1$（影响区间 $[1, 2]$）和操作 $3$（影响区间 $[3, 5]$）。执行这两个操作后，商品库存序列变为 $[1, 1, 1, 1, 1]$。在这种情况下，所有商品的库存量都不为 $0$。因此，库存量为 $0$ 的商品种类数为 $0$。

• 不执行操作 $3$：剩余的操作是操作 $1$（影响区间 $[1, 2]$）和操作 $2$（影响区间 $[2, 4]$）。执行这两个操作后，商品库存序列变为 $[1, 2, 1, 1, 0]$。在这种情况下，只有编号为 $5$ 的商品的库存量为 $0$。因此，库存量为 $0$ 的商品种类数为 $1$。

【评测用例规模与约定】

对于 $20\%$ 的评测用例，$1 \le n,m \le 5 \times 10^3$，$1\le L \le R \le n$。
对于所有评测用例，$1 \le n,m \le 3 \times 10^5$，$1 \le L \le R \le n$。

解决方案

这道题涉及了区间的计算，而在需要频繁进行区间更新的场景中，差分数组可以提供高效的解决方案。

关于差分在区间计算中的特殊性可以由下边这个简单的示例来说明：

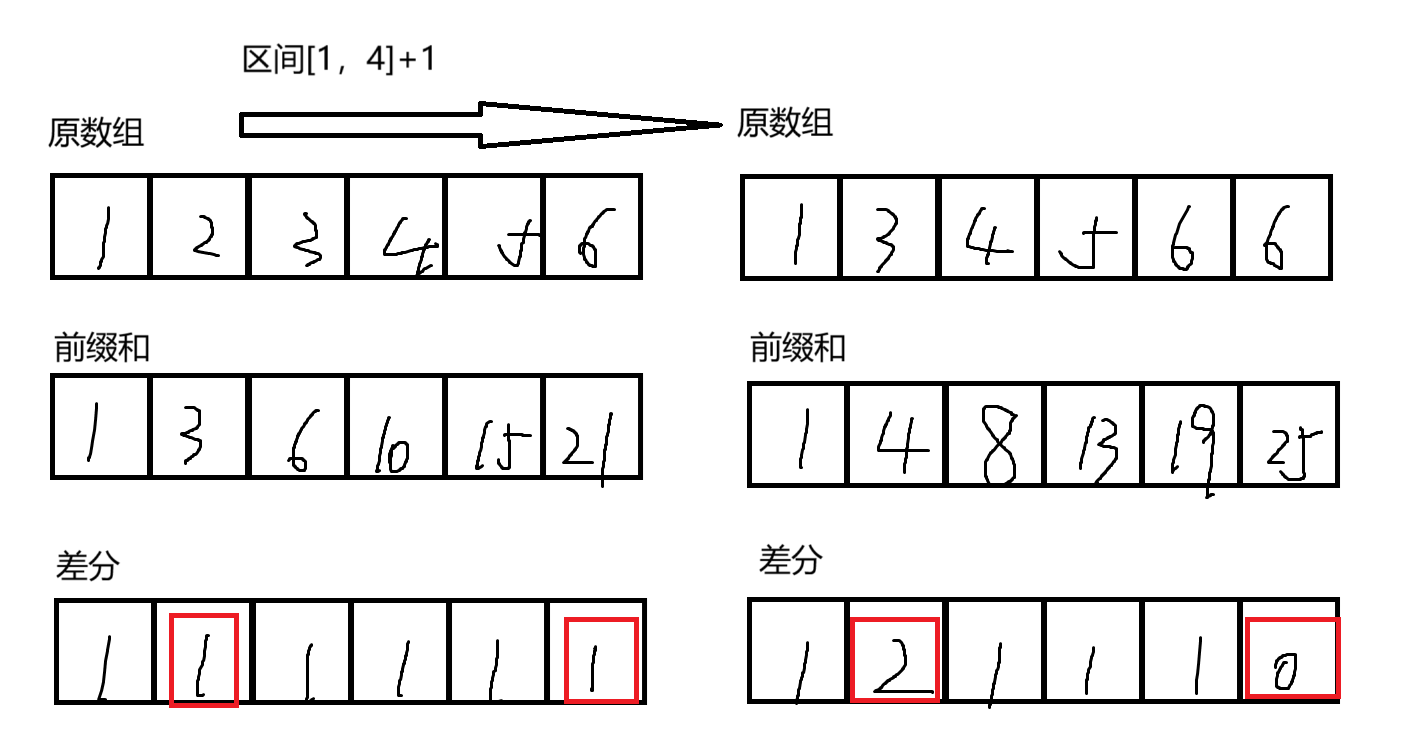
不难发现，若对原数组区间[l,r]整体加上一个k，则对于其差分数组b来说，就是b[l] += 1，b[r+1] -= 1。随后再对该差分数组进行前缀和运算即可得到原数组。

那么我们也就得到了对于此题的解决方案：

def main():
  lrs = []
  n, m = map(int, input().split())
  for i in range(m):
    l, r = map(int, input().split())
    lrs.append((l, r))

  # 枚举每一种区间不进行操作的情况
  for i in range(m):
    lrs_copy = lrs[:i]+lrs[i+1:]

    goods = [0] * (n + 5)

    # 得到差分数组
    for j in range(1, n+1):
      goods[i] -= goods[i-1]
    # 对边界值进行加减
    for l, r in lrs_copy:
      goods[l-1] += 1
      goods[r] -= 1
    # 进行前缀和以得到原数组
    for j in range(1, n+1):
      goods[j] += goods[j-1]

    #输出最终库存量为0的商品种类数
    print(goods[:n].count(0))

if __name__ == "__main__":
  main()

需要注意的是，这段代码的时间复杂度较高，但这里我们仅用于掌握差分的思想，不再对其进行优化。