基础图论_Floyd算法的Python实现

Floyd算法和Dijkstra算法是图论中最经典的两种求最短路径的算法，但亦有所不同。前者主要聚焦与一个确定的起点与不同的终点之间的最短路径，而后者则可以求出任意两点间的最短路径。

下面我们就以两道蓝桥杯真题为例。

蓝桥公园

题目描述

小明喜欢观景，于是今天他来到了蓝桥公园。

已知公园有 N 个景点，景点和景点之间一共有 M 条道路。小明有 Q 个观景计划，每个计划包含一个起点 st 和一个终点 ed，表示他想从 st 去到 ed。但是小明的体力有限，对于每个计划他想走最少的路完成，你可以帮帮他吗？

输入描述

输入第一行包含三个正整数 N,M,Q

第 2 到 M+1 行每行包含三个正整数 u,v,w，表示 u↔v 之间存在一条距离为 w 的路。

第 M+2 到 M+Q−1 行每行包含两个正整数 st,ed，其含义如题所述。

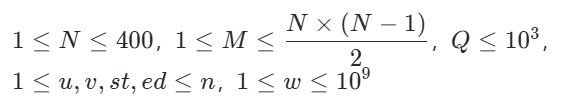
输出描述

输出共 Q 行，对应输入数据中的查询。

若无法从 st 到达 ed 则输出 −1。

输入输出样例

示例 1

输入

3 3 3
1 2 1
1 3 5
2 3 2
1 2
1 3
2 3

输出

1
3
2

运行限制

• 最大运行时间：3s
• 最大运行内存: 128M

解决方案

Floyd算法的特点在于通过一个中间节点k来更新两个其它节点i和j间的最短路径，如果我们用数组arr来存储路径信息的话，那么不难想出状态转移方程应该为arr[i][j] = min(arr[i][j], arr[i][k] + arr[k][j])。（这里就是一种动态规划的思想）

INF = float('inf')

def Floyd(arr, n):
    for k in range(1, n+1):
        for i in range(1, n+1):
            for j in range(1, n+1):
                arr[i][j] = min(arr[i][j], arr[i][k] + arr[k][j])

def main():
    n, m, q = map(int, input().split())

    arr = [[INF for _ in range(n+1)] for __ in range(n+1)]
    for i in range(m):
        u, v, w = map(int, input().split())
        arr[u][v] = arr[v][u] = min(arr[u][v], w)

    Floyd(arr, n)

##    for i in range(n+1):
##        for j in range(n+1):
##            print(arr[i][j], end=" ")
##        print("\n")

    for i in range(q):
        st, ed = map(int, input().split())
        if arr[st][ed] == INF:
            print(-1)
        elif st == ed:
            print(0)
        else:
            print(arr[st][ed])

if __name__ == "__main__":
    main()

Bingo!