优先队列的应用

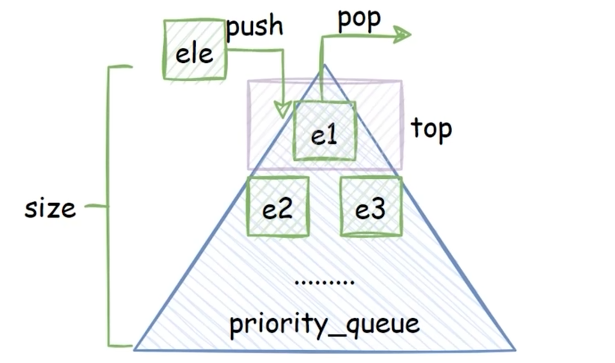
优先队列是一种基于堆实现的数据结构，它使得队列中最高优先级的元素总是排在堆顶（优先级或大或小，与大顶堆或小顶堆有关）。

在Python中可以直接使用heapq库来使用优先队列，主要有以下几个用法:

import heapq
import sys

heap = list(map(int, sys.stdin.readline().strip().split()))

heap = heapq.heapify(heap)      # 将一个朴素队列堆化
min_num = heapq.heappop(heap)   # 弹出堆中的最小元素（该库默认定义为小顶堆）

heapq.heappush(heap, new_num)   # 插入一个新的数

n = 3
heap = [1, 3, 5, 7, 2, 4, 6, 8]
print(heapq.nsmallest(n, heap)) # 输出堆中最小的n个元素
print(heapq.nlargest(n, heap))  # 输出堆中最大的n个元素

最大堆可以通过将队列全部取相反数实现，不再赘述。

P1090 [NOIP 2004 提高组] 合并果子

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 $n-1$ 次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 $1$ ，并且已知果子的种类 数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 $3$ 种果子，数目依次为 $1$ ， $2$ ， $9$ 。可以先将 $1$ 、 $2$ 堆合并，新堆数目为 $3$ ，耗费体力为 $3$ 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 $12$ ，耗费体力为 $12$ 。所以多多总共耗费体力 $=3+12=15$ 。可以证明 $15$ 为最小的体力耗费值。

输入格式

共两行。
第一行是一个整数 $n(1\leq n\leq 10000)$ ，表示果子的种类数。

第二行包含 $n$ 个整数，用空格分隔，第 $i$ 个整数 $a_i(1\leq a_i\leq 20000)$ 是第 $i$ 种果子的数目。

输出格式

一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 $2^{31}$ 。

输入输出样例 #1

输入 #1

3 
1 2 9

输出 #1

15

说明/提示

对于 $30\%$ 的数据，保证有 $n \le 1000$：

对于 $50\%$ 的数据，保证有 $n \le 5000$；

对于全部的数据，保证有 $n \le 10000$。

解决方案

直接逐个弹出最小的两个元素，并将这两个元素的和再插入回堆中即可。

import heapq
import sys

def main():
    n = int(input())
    heap = list(map(int, sys.stdin.readline().strip().split()))

    heapq.heapify(heap)

    ans = 0
    while len(heap) > 1:
        pop_num1 = heapq.heappop(heap)
        pop_num2 = heapq.heappop(heap)

        push_num = pop_num1 + pop_num2
        ans += push_num

        heapq.heappush(heap, push_num)
        
    print(ans)
    

if __name__ == "__main__":
    main()

Bingo!

这里留个尾巴，等主播打完蓝桥杯回来更新P8755